4 First-Order Circuits
4.1 Dynamic Analysis RC Circuit
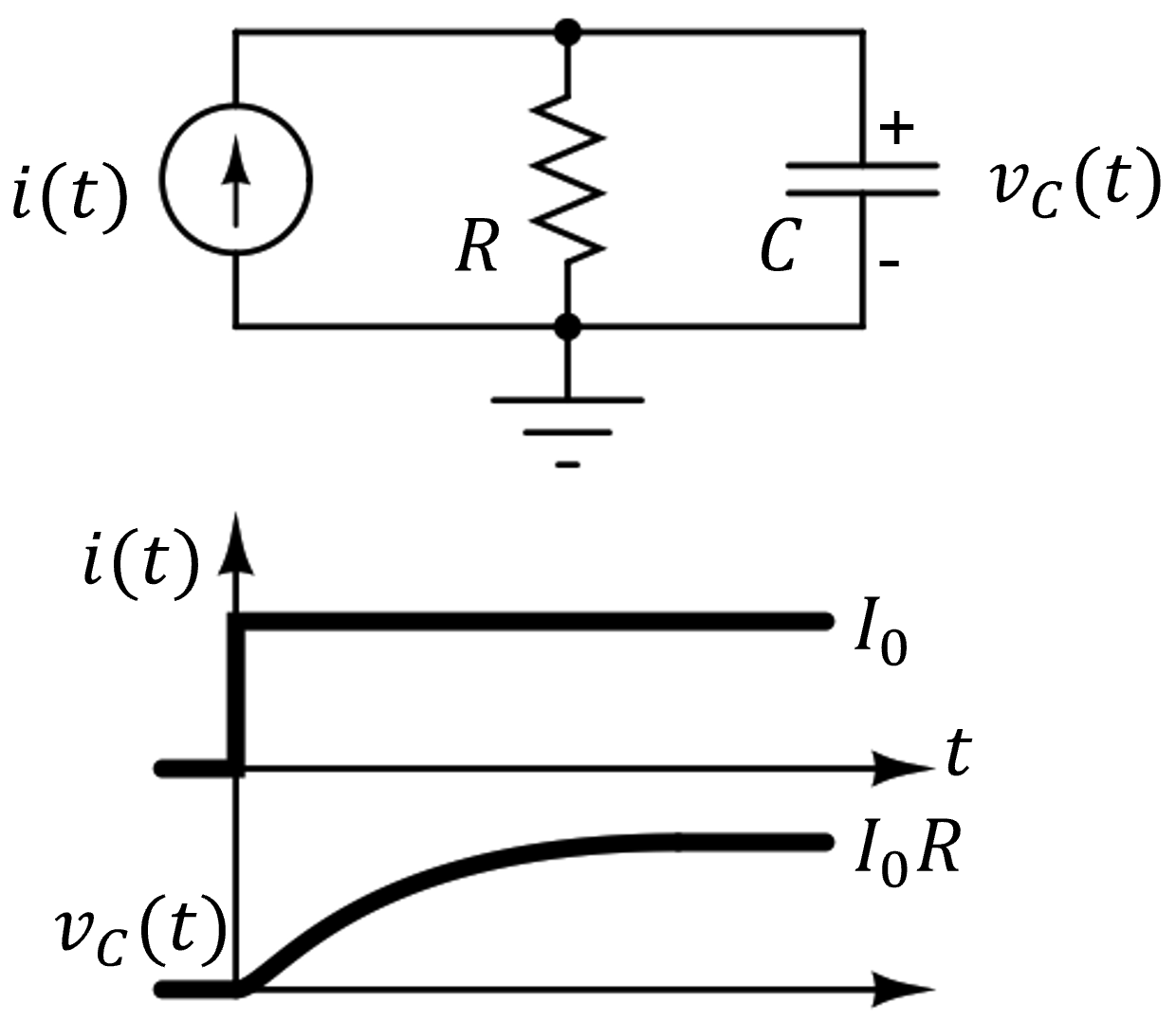
The node analysis for the parallel RC circuit yields:
\[ i(t) = \frac{v_C}{R} + C \frac{dv_C}{dt} \]
Or, rewritten as:
\[ \frac{dv_C}{dt} + \frac{v_C}{RC} = \frac{i(t)}{C} \]
This is a linear differential equation with constant coefficients.
The complete solution consists of two parts:
- Homogeneous Solution
- Particular Solution
The overall solution is the sum of these two parts.
The homogeneous equation:
\[ \frac{dv_{CH}}{dt} + \frac{v_{CH}}{RC} = 0 \]
Assume \(v_{CH} = Ae^{st}\):
Substituting and solving gives:
\[ s = -\frac{1}{RC} \]
So,
\[ v_{CH} = A e^{-t/RC} \]
- Product \(RC\) has dimension of time called time-constant .
Particular Solution
For a constant input current \(I_0\):
\[ I_0 = \frac{v_{cp}}{R} + C \frac{dv_{cp}}{dt} \]
Assume \(v_{CP} = K\):
Substitute into the equation:
\[ v_{CP} = I_0 R \]
Complete Solution
Combine both solutions:
\[ v_C = A e^{-t/RC} + I_0 R \]
Apply initial condition at \(t = 0\):
\[ A = -I_0 R \]
Thus,
\[ v_C = -I_0 R e^{-t/RC} + I_0 R \]
or
\[ v_C = I_0 R (1 - e^{-t/RC}) \]
Effect of RC Value
- Small RC: Faster charging, steeper curve.
- Large RC: Slower charging, gradual curve.
Discharge Transient
For the discharge case (homogeneous solution):
- Initial condition: \(v_C = I_0 R\) at \(t = 0\)
- Solution:
\[ v_C = I_0 R e^{-t/RC} \]
General Form
\[ v_C = v_C(0) e^{-t/RC} \]
Properties of the Exponential Decay
- For \(x = A e^{-t/\tau}\), the initial slope at \(t = 0\):
\[ \left. \frac{dx}{dt} \right|_{t=0} = -\frac{A}{\tau} \]
- At \(t = \tau\):
\[ x(\tau) = \frac{A}{e} \]
- Time to go from 90% to 10%:
\[ t_{90\%} - t_{10\%} = RC \ln\left(\frac{0.9}{0.1}\right) = 2.2\tau \]
Summary Table
| Parameter | Formula | Notes |
|---|---|---|
| Time Constant (\(\tau\)) | \(RC\) | Determines response speed |
| Charging Voltage | \(I_0 R (1 - e^{-t/RC})\) | Step input |
| Discharge Voltage | \(v_C(0) e^{-t/RC}\) | Initial voltage \(v_C(0)\) |
| Initial Slope | \(-A/\tau\) | At \(t = 0\) |
| 90%-10% Time Span | \(2.2\tau\) | Exponential decay |
Notes
- The exponential response is a hallmark of first-order RC circuits.
- The time constant \(RC\) is critical for determining how quickly the voltage changes in response to a step input or discharge.